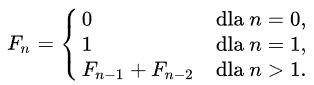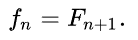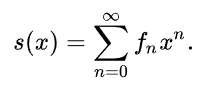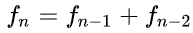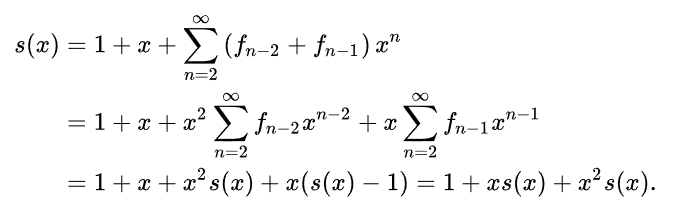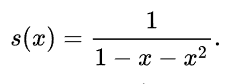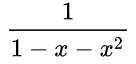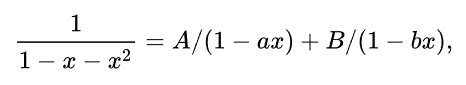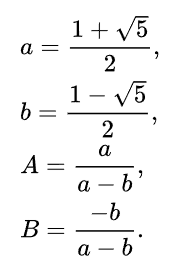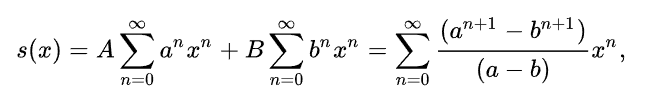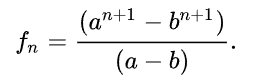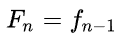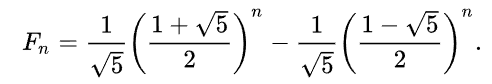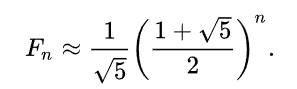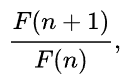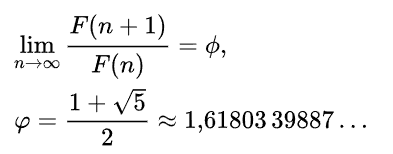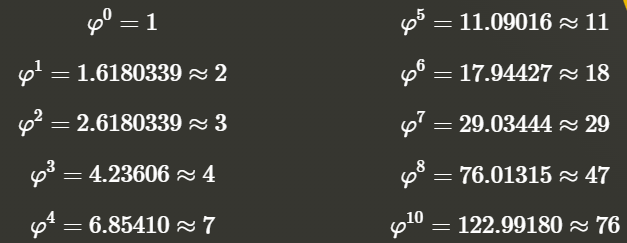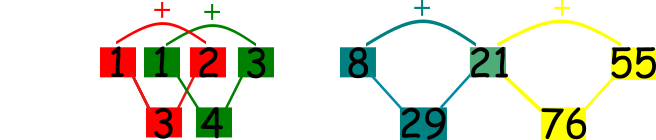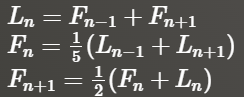Ciag Fibonacciego
Opis
Ciąg Fibonacciego – ciąg liczb naturalnych określony rekurencyjnie w sposób następujący:
Pierwszy wyraz jest równy 0, drugi jest równy 1, każdy następny jest sumą dwóch poprzednich.
Formalnie:
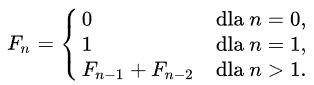
Kolejne wyrazy tego ciągu nazywane są liczbami Fibbonacciego. Zaliczanie zera do elementów ciągu Fibonacciego zależy od umowy - część autorów definiuje ciąg od F1 = F2 = 1.
Pierwsze dwadzieścia wyrazów ciągu Fibonacciego to:
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 |
F10 | F11 | F12 | F13 | F14 | F15 | F16 | F17 | F18 | F19 |
| 0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
144 |
233 |
377 |
610 |
987 |
1597 |
2584 |
4181 |
Ciąg został omówiony w roku 1202 przez Leonarda z Pizy, zwanego Fibonaccim,
w dziele Liber abaci jako rozwiązanie zadania o rozmnażaniu się królików. Nazwę „ciąg Fibonacciego” spopularyzował w XIX w. Édouard Lucas.
Wzór Bineta
Jawny wzór na n-ty wyraz ciągu Fibonacciego podany w 1843 r. przez J.P.M. Bineta możemy otrzymać, korzystając z metody funkcji tworzących.
Niech
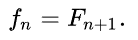
Funkcja tworząca dla tego ciągu ma postać
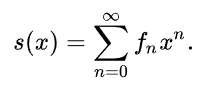
Podstawiając
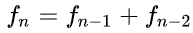
otrzymujemy:
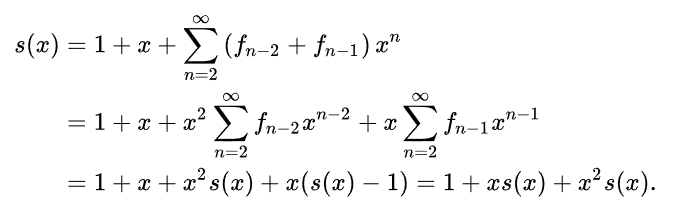
W szczególności,
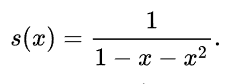
Wyrażenie
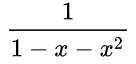
można przedstawić w prostszej postaci, mianowicie:
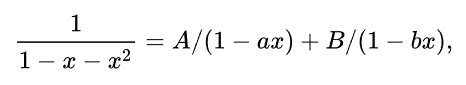
gdzie:
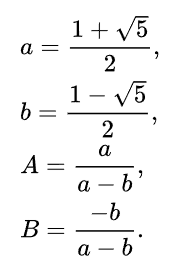
Wówczas:
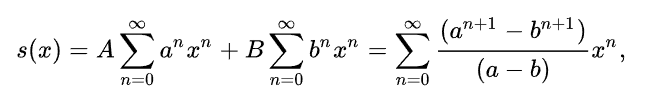
a stąd:
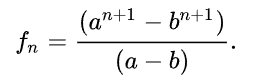
Ponieważ
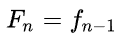
wyprowadzony został ostatecznie tzw. wzór Bineta zwany czasem wzorem Eulera-Bineta:
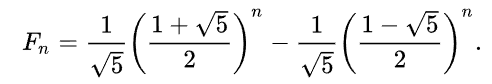
Ponieważ drugi człon tego wyrażenia szybko zbiega do zera
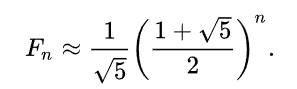
Własności
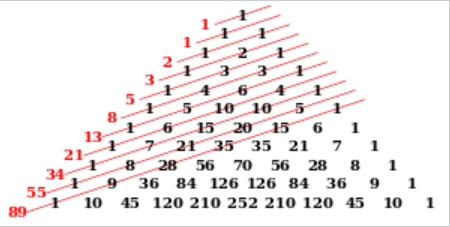
Sumy wyrazów tworzące ciąg Fibonacciego na trójkącie Pascala.
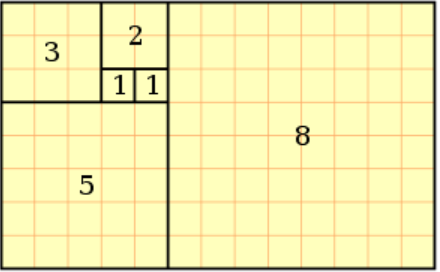
Ciąg kwadratów, których długości boków są kolejnymi liczbami Fibonacciego
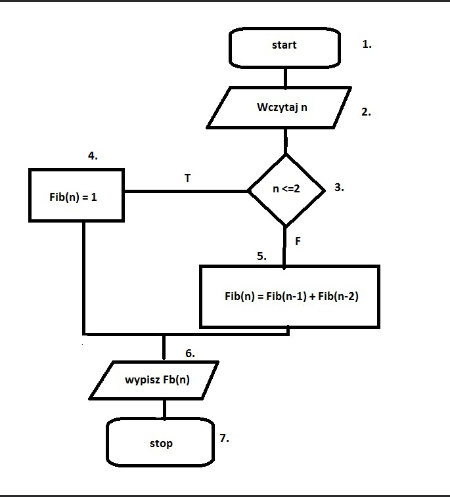
Obliczanie liczb Fibonacciego
Teoretycznie wartości kolejnych wyrazów ciągu Fibonacciego mogą być obliczone wprost z definicji, jest to jednak metoda na tyle wolna,
że stosowanie jej ma tylko sens dla niewielu początkowych wyrazów ciągu, nawet na bardzo szybkich komputerach. Wynika to z tego, że definicja Fn
wielokrotnie odwołuje się do wartości poprzednich wyrazów ciągów. Drzewo wywołań takiego algorytmu dla parametru n musi co najmniej Fn liści o wartości 1.
Ponieważ ciąg Fibonacciego rośnie wykładniczo, oznacza to wyjątkowo słabą wydajność.
Istnieje równie prosta i znacznie szybsza metoda. Obliczamy wartości ciągu po kolei: F0,F1,F2 i tak aż do Fn, za każdym razem korzystając z tego, co już obliczyliśmy.
Nie trzeba nawet zapamiętywać wszystkich obliczonych dotychczas wartości, ponieważ wystarczą dwie ostatnie. Daje to złożoność liniową – o wiele lepszą od wykładniczej
złożoności poprzedniej metody. Metoda ta może być postrzegana jako zastosowanie programowania dynamicznego.
Złota liczba
Granica ciągu (wartość, w której dowolnym otoczeniu znajdują się prawie wszystkie (tzn. wszystkie poza co najwyżej skończenie wieloma) wyrazy danego ciągu. Inaczej – wartość,
dowolnie blisko której leżą wszystkie wyrazy ciągu o dostatecznie dużych wskaźnikach.):
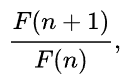
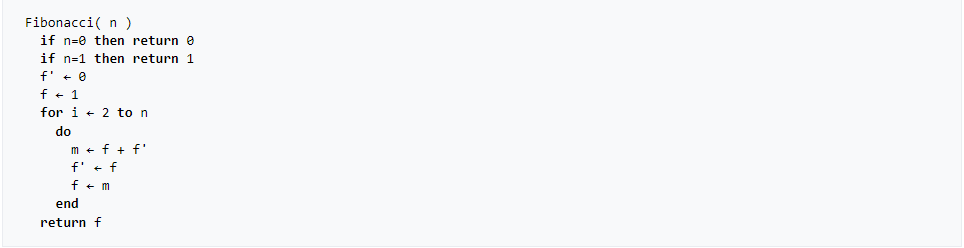
czyli ilorazów sąsiadujących ze sobą wyrazów ciągu Fibonacciego, to tzw. złota liczba lub złota proporcja definiowana jako dodatnie rozwiązanie równania:

czyli
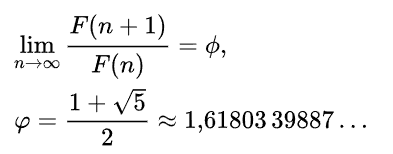
Ciąg Lucasa
Ciąg Lucasa to, po ciągu Fibonacciego, najbardziej znany ciąg powstały na podobnej zasadzie.
Lucas poświęcił sporo czasu na badanie ciągu Fibonacciego i stworzył ciąg jeszcze bliżej związany ze złotą proporcją.
Odpowiedział na pytanie co się stanie gdy zaokrąglimy kolejne potęgi złotej liczby:
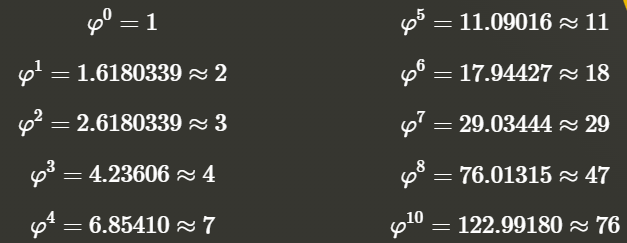
Zauważ, że kolejne wyniki zaokrągleń powstają po zsumowaniu dwóch poprzednich.
Fraktalna natura ciągu Fibonacciego
Zaobserwuj co się stanie kiedy zestawimy ze sobą ciąg Fibonacciego i Lucasa:
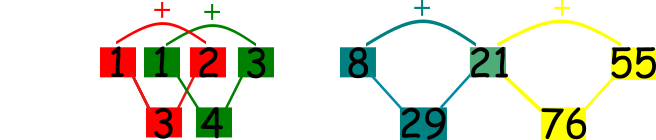
Zauważ, że zachodzą równości:
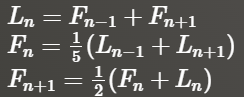
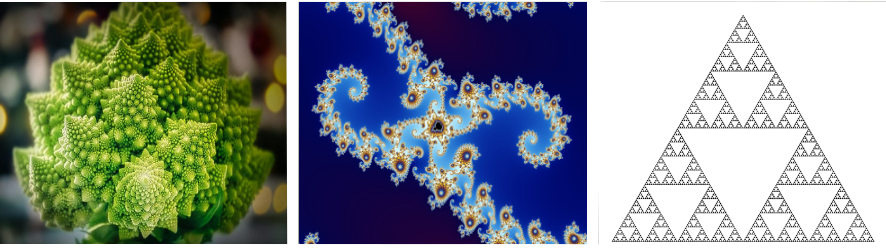
Fraktal to rodzaj figury geometrycznej charakteryzującej się własnością samopodobieństwa — małe fragmenty fraktala, oglądane w odpowiednim powiększeniu,
wyglądają tak samo jak obiekt pierwotny.
W przypadku tych dwóch ciągów udało nam się dokonać zamiany transponowania jednego ciągu w drugi zgodnie z regułą samopodobieństwa. Poniżej znajdują się przykłady fraktali.
Graficzna reprezentacja dwójkowa
Jeśli kolejne wyrazy ciągu zapisać w systemie dwójkowym, jeden pod drugim, z wyrównaniem do prawej strony, to otrzymamy wydłużający się w dół trójkąt, którego elementy powtarzają się
(„czubek” pojawia się poniżej, przy prawej krawędzi, w coraz dłuższym rozwinięciu – pojawia się nad nim „biały trójkąt”), co czyni go podobnym do fraktala. Dla lepszej przejrzystości
na rysunku obok wszystkie zera zastąpiono białymi punktami, a jedynki – czarnymi.

Liczby pierwsze w ciągu Fibonacciego
Niektóre z wyrazów ciągu Fibonacciego to liczby pierwsze, początkowe to: 2, 3, 5, 13, 89, 233, 1597, 28657, 514229.
Problem, czy w ciągu Fibonacciego istnieje nieskończenie wiele liczb pierwszych, jak dotąd nie doczekał się rozstrzygnięcia (stan na styczeń 2023).
Powrót do głównej strony